BASIC DEFINITION AND UTILITY OF PERCENTAGE
Percent literally, means ‘for every 100’ and is derived from the French word ‘cent’, which is French for 100. The basic utility of Percentage arises from the fact that it is one of the most powerful tools for comparison of numerical data and information. It is also one of the simplest tools for comparison of data. In the context of business and economic performance, it is specifically useful for comparing data such as profits, growth rates, performance, magnitudes and so on.
Mathematical definition of percentage
The concept of percentage mainly applies to ratios, and the percentage value of a ratio is arrived at by multiplying by 100 the decimal value of the ratio.
For example, a student scores 20 marks out of a maximum possible 30 marks. His marks can then be denoted as 20 out of 30 = (20/30) or (20/30) × 100% = 66.66%.
The process for getting this is perfectly illustrated through the unitary method:
Then the value of x × 30 = 20 × 100
x = (20/30) × 100 Æ the percentage equivalent of a ratio.
Now, let us consider a classic example of the application of percentage:
Example: Student A scores 20 marks in an examination out of 30 while another student B scores 40 marks out of 70. Who has performed better?
Solution: Just by considering the marks as 20 and 40, we do not a get clear picture of the actual performance of the two students. In order to get a clearer picture, we consider the percentage of marks.
Thus, A gets (20/30) × 100 = 66.66%
While B gets (40/70) × 100 = 57.14%
Now, it is clear that the performance of A is better.
Consider another example:
Example: Company A increases its sales by 1 crore rupees while company B increases its sales by 10 crore rupees. Which company has grown more?
Solution: Apparently, the answer to the question seems to be company B. The question cannot be answered since we don’t know the previous year’s sales figure (although on the face of it Company B
seems to have grown more). If we had further information saying that company A had a sales turnover of ` 1 crore in the previous year and company B had a sales turnover of ` 100 crore in the previous year, we can compare growth rates and say that it is company A that has grown by 100%. Hence, company A has a higher growth rate, even though in terms of absolute value increase of sales, company B has grown much more.
IMPORTANCE OF BASE / DENOMINATOR FOR PERCENTAGE CALCULATIONS
Mathematically, the percentage value can only be calculated for ratios that, by definition, must have a
denominator. Hence, one of the most critical aspects of the percentage is the denominator, which in other words is also called the base value of the percentage. No percentage calculation is possible without knowing the base to which the percentage is to be calculated.
Hence, whenever faced with the question ‘What is the percentage …?’ always try first to find out the
answer to the question ‘Percentage to what base?’
CONCEPT OF PERCENTAGE CHANGE
Whenever the value of a measured quantity changes, the change can be captured through
(a)Absolute value change or
(b)Percentage change.
Both these measurements have their own advantages and disadvantages.
Absolute value change: It is the actual change in the measured quantity. For instance, if sales in year 1 is ` 2500 crore and the sales in year 2 is ` 2600 crore, then the absolute value of the change is ` 100 crore.
Percentage change: It is the percentage change got by the formula
As seen earlier, this often gives us a better picture of the effect of the change.
Note: The base used for the sake of percentage change calculations is always the original quantity unless otherwise stated.
Example: The population of a city grew from 20 lakh to 22 lakh. Find the
(a) percentage change
(b) percentage change based on the final value of population
Solution:
(a) percentage change = (2/20) × 100 = 10%
(b) percentage change on the final value = (2/22) × 100 = 9.09%
Difference between the Percentage Point Change and the Percentage Change
The difference between the percentage point change and the percentage change is best illustrated through an example. Consider this:
The savings rate as a percentage of the GDP was 25% in the first year and 30% in the second year.
Assume that there is no change in the GDP between the two years. Then:
Percentage point change in savings rate = 30% – 25% = 5 percentage points.
Percentage change in savings rate = [(30-25) / 25] x 100 = 25%
PERCENTAGE RULE FOR CALCULATING PERCENTAGE VALUES THROUGH ADDITIONS
Illustrated below is a powerful method of calculating percentages. In my opinion, the ability to calculate percentage through this method depends on your ability to handle 2 digit additions. Unless you develop the skill to add 2 digit additions in your mind, you are always likely to face problems in calculating percentage through the method illustrated below. In fact, trying this method without being strong at 2-digit additions/subtractions (including 2 digits after decimal point) would prove to be a disadvantage in your attempt at calculating percentages fast.
This process, essentially being a commonsense process, is best illustrated through a few examples:
Example: What is the percentage value of the ratio: 53/81?
Solution: The process involves removing all the 100%, 50%, 10%, 1%, 0.1% and so forth of the
denominator from the numerator.
Thus, 53/81 can be rewritten as: (40.5 + 12.5)/81 = 40.5/81 + 12.5/81 = 50% + 12.5/81
= 50% + (8.1 + 4.4)/81 = 50% + 10% + 4.4/81
= 60% + 4.4/81
At this stage you know that the answer to the question lies between 60 – 70% (Since 4.4 is less than 10% of 81) At this stage, you know that the answer to the calculation will be in the form: 6a.bcde ….
All you need to do is find out the value of the missing digits.
In order to do this, calculate the percentage value of 4.4/81 through the normal process of multiplying the numerator by 100.
Thus the % value of = 4.4/81 = (4.4 x 100)/81 = 440/81
[Note: Use the multiplication by 100, once you have the 10% range. This step reduces the decimal
calculations.]
Thus 440/81= 5% with a remainder of 35
Our answer is now refined to 65.bcde. (1% Range)
Next, in order to find the next digit (first one after the decimal add a zero to the remainder;
Hence, the value of ‘b’ will be the quotient of b Æ 350/81 = 4 Remainder 26
Answer: 65.4cde (0.1% Range)
c Æ 260/81 = 3 Remainder 17
Answer: 65.43 (0.01% Range)
and so forth.
The advantages of this process are two fold:
(1) You only calculate as long as you need to in order to eliminate the options. Thus, in case there was only a single option between 60 – 70% in the above question, you could have stopped your
calculations right there.
(2) This process allows you to go through with the calculations as long as you need to. However, remember what I had advised you right at the start: Strong Addition skills are a primary requirement for using this method properly.
To illustrate another example:
What is the percentage value of the ratio 223/72 ?
223/72 Æ 300 – 310% Remainder 7
700/72 Æ 9. Hence 309 – 310%, Remainder 52
520/72 Æ 7. Hence, 309.7, Remainder 16
160/72 Æ 2. Hence, 309.72 Remainder 16
Hence, 309.7222 (2 recurs since we enter an infinite loop of 160/72 calculations).
In my view, percentage rule (as I call it) is one of the best ways to calculate percentages since it gives you the flexibility to calculate the percentage value up to as many digits after decimals as you are required to and at the same time allows you to stop the moment you attain the required accuracy range.
Effect of a Percent Change in the Numerator on a Ratio’s Value
The numerator has a direct relationship with the ratio, that is, if the numerator increases the ratio increases. The percentage increase in the ratio is the same as the percentage increase in the numerator, if the denominator is constant.
Thus, 22/40 is exactly 10% more than 20/40. (in terms of percentage change)
Percentage Change Graphic and its Applications
In mathematics there are many situations where one is required to work with percentage changes. In such situations the following thought structure (Something I call Percentage Change Graphic) is a very useful tool:
What I call Percentage Change Graphic (PCG) is best illustrated through an example:
Suppose you have to increase the number 20 by 20%. Visualise this as follows:
The PCG has 6 major applications listed and explained below: PCG applied to:
1. Successive changes
2. Product change application
3. Product constancy application
4. A Æ BÆA application
5. Denominator change to Ratio Change application
6. Use of PCG to calculate Ratio Changes
Application 1: PCG Applied to Successive Changes
This is a very common situation in most questions.
Suppose you have to solve a question in which a number 30 has two successive percentage increases
(20% and 10% respectively). The situation is handled in the following way using PCG:
Illustration
A’s salary increases by 20% and then decreases by 20%. What is the net percentage change in A’s salary?
Solution:
Hence, A’s salary has gone down by 4%
Illustration
A trader gives successive discounts of 10%, 20% and 10% respectively. The percentage of the original cost price he will recover is:
Solution:
Hence the overall discount is 35.2% and the answer is 64.8%.
Illustration
A trader marks up the price of his goods by 20%, but to a particularly haggling customer he ends up giving a discount of 10% on the marked price. What is the percentage profit he makes?
Solution:
Hence, the percentage profit is 8%.
Application 2: PCG applied to Product Change
Suppose you have a product of two variables say 10 × 10.
If the first variable changes to 11 and the second variable changes to 12, what will be the percentage
change in the product? [Note there is a 10% increase in one part of the product and a 20% increase in the other part.]
The formula given for this situation goes as: (a + b + ab/100)
Hence, Required % change = 10 + 20 + (10 x 20) / 100
(Where 10 and 20 are the respective percentage changes in the two parts of the product)
However, a much easier solution for this case can be visualized as:
Hence, the final product shows a 32% increase.
Similarly suppose 10 × 10 × 10 becomes 11 × 12 × 13
In such a case the following PCG will be used:
Hence, the final product sees a 71.6 percent increase
(Since, the product changes from 100 to 171.6)
Note: You will get the same result irrespective of the order in which you use the respective percentage changes. Also note that this process is very similar to the one used for calculating successive percentage change.
Application for DI:
Suppose you have two pie charts as follows:
If you are asked to calculate the percentage change in the sales revenue of scooters for the company from year one to year two, what would you do?
The formula for percentage change would give us:
Obviously this calculation is easier said than done.
However, the Product change application of PCG allows us to execute this calculation with a lot of ease comparatively. Consider the following solution:
Product for year one is: 0.2347 × 17342.34
Product for year two is: 0.2655 × 19443.56
These can be approximated into:
234 × 173 and 265 × 194 respectively (Note that by moving into three digits we do not end up losing any accuracy. We have elaborated this point in the chapter on Ratio and Proportions.)
The overall percentage change depends on two individual percentage changes:
234 increases to 265: A % change of 31/234 = 13.2 % approx. This calculation has to be done using the percentage rule for calculating the percentage value of the ratio 173 increases to 194 – A percentage change of approximately 12%.
Thus PCG will give the answer as follows:
Hence, 26.76 % increase in the product’s value. (Note that the value on the calculator for the full calculation sans any approximations is 26.82 %, and given the fact that we have come extremely close to the answer—the method is good enough to solve the question with a reasonable degree of accuracy.)
Application 3 of PCG: Product Constancy Application (Inverse proportionality)
Suppose you have a situation wherein the price of a commodity has gone up by 25%. In case you are required to keep the total expenditure on the commodity constant, you would obviously need to cut down on the consumption. By what percentage? Well, PCG gives you the answer as follows:
Hence, the percentage drop in consumption to offset the price increase is 20%.
I leave it to the student to discover the percentage drop required in the second part of the product if one part increases by 50 percent.
Note: Product constancy is just another name for Inverse proportionality.
Application 4 of PCG: A Æ B Æ A.
Very often we are faced with a situation where we compare two numbers say A and B. In such cases, if we are given a relationship from A to B, then the reverse relationship can be determined by using PCG in much the same way as the product constancy use shown above.
B’s salary is 25% more than A’s salary. By what percent is A’s salary less than B’s salary?
A drop of 25 on 125 gives a 20% drop.
Hence A’s salary is 20% less than B’s.
Note: The values which applied for Product Constancy also apply here.
Application 5 of PCG Æ Effect of change in Denominator on the Value of the Ratio
The denominator has an inverse relationship with the value of a ratio.
Hence the process used for product constancy (and explained above) can be used for calculating
percentage change in the denominator.
For instance, suppose you have to evaluate the difference between two ratios:
Ratio 1 : 10/20
Ratio 2 : 10/25
As is evident the denominator is increasing from 20 to 25 by 25%.
If we calculate the value of the two ratios we will get:
Ratio 1 = 0.5, Ratio 2 = 0.4.
% change between the two ratios = 0.1 / 0.5 × 100 = 20% Drop
This value can be got through PCG as:
100 --> 125 --> 100
Hence, 20% drop.
Note: This is exactly the same as Product constancy and works here because the numerator is constant.
Hence, R1 = N/D1 and R2 = N/D2
i.e. R1 × D1 = N and R2 × D2 = N, which is the product constancy situation.
Direct process for calculation
To find out the percentage change in the ratio due to a change in the denominator follow the following process:
In order to find the percentage change from 10/20 to 10/25, calculate the percentage change in the denominator in the reverse fashion.
i.e. The required percentage change from R1 to R2 will be given by calculating the percentage change in the denominators from 25 to 20 (i.e. in a reverse fashion) & not from 20 to 25.
Product Constancy Table, Inverse Proportionality Table, A Æ B Æ A table, Ratio Change to Denominator table
Application 6: Use of PCG to Calculate Ratio Changes:
Under normal situations, you will be faced with ratios where both numerator and denominator change.
The process to handle and calculate such changes is also quite convenient if you go through PCG.
Calculate the percentage change between the Ratios.
Ratio 1 = 10/20 Ratio 2 = 15/25
The answer in this case is 0.5 Æ 0.6 (20% increase). However, in most cases calculating the values of
the ratio will not be easy. The following PCG process can be used to get the answer:
When 10/20 changes to 15/25, the change occurs primarily due to two reasons:
(A) Change in the numerator (Numerator effect)
(B) Change in the denominator (Denominator effect)
By segregating the two effects and calculating the effect due to each separately, we can get the answer easily as follows:
Numerator Effect
The numerator effect on the value of the ratio is the same as the change in the numerator. Hence, to calculate the numerator effect, just calculate the percentage change in the numerator:
In this case the numerator is clearly changing from 10 to 15 (i.e. a 50% increase.) This signifies that the numerator effect is also 50%.
Denominator Effect
As we have just seen above, the effect of a percentage change in the denominator on the value of the ratio is seen by calculating the denominator’s percentage change in the reverse order.
In this case, the denominator is changing from 20 to 25. Hence the denominator effect will be seen by
going reverse from 25 to 20 i.e. 20% drop.
With these two values, the overall percentage change in the Ratio is seen by:
This means that the ratio has increased by 20%.
Implications for Data Interpretation
Percentage is perhaps one of the most critical links between QA and Data Interpretation. In the chapter theory mentioned above, the Percentage Rule for Percentage Calculations and the PCG applied to product change and ratio change are the most critical.
As already shown, the use of PCG to calculate the percentage change in a product (as exhibited through the pie chart example above) as well as the use of PCG to calculate ratio changes are two extremely useful applications of the concepts of percentages into DI.
Applying Percentages for the special case of comparing two ratios to find the larger one.
Suppose you have two ratios to compare. Say R1 = N1/D1 and R2 = N2/D2
The first step is to find the ten percent ranges for each of these ratios. In case, they belong to different ranges of 10% (say R1 lies between 50-60 while R2 lies between 70 to 80), it becomes pretty simple to say which one will be higher.
In case, both of these values for percentage of the ratios belong to the same ten percent range, then we can use the following process
Step 1: Calculate the percentage change in the numerator
Step 2: Calculate the percentage change in the denominator. There could be four cases in this situation, when we move from Ratio1 to Ratio2:
Case 1: Numerator is increasing while denominator is decreasing Æ obviously the net effect of the two changes will be an increase in the ratio. Hence, R2 will be greater.
Case 2: Numerator is decreasing while denominator is increasing Æ obviously the net effect of the two changes will be a decrease in the ratio. Hence, R1 will be greater. It is only in the following cases that we need to look at the respective changes in the numerator and denominator.
Case 3: Numerator and denominator are both increasing Calculate the percentage value of the respective increases. If the numerator is increasing more than the denominator the ratio will go up. On the other hand, if the denominator is increasing more than the numerator, Ratio2 will be smaller than Ratio1. (Note: Compare in percentage values)
Case 4: Numerator and denominator are both decreasing Æ Calculate the percentage value of the respective decreases. If the numerator is decreasing more than the denominator the ratio will go down. On the other hand, if the denominator is decreasing more than the numerator, Ratio2 will be greater than Ratio1.
FRACTION TO PERCENTAGE CONVERSION TABLE
The following percentage values appear repeatedly over the entire area where questions can be framed on the topic of percentage. Further, it would be of great help to you if you are able to recognize these values separately from values that do not appear in the following table.
Some Utilisations of the Table
• The values that appear in the table are all percentage values. These can be converted into decimals by just shifting the decimal point by two places to the left. Thus, 83.33% = 0.8333 in decimal value.
• A second learning from this table is in the process of division by any of the numbers such as 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 15, 16, 24 and so on, students normally face problems in calculating the decimal values of these divisions. However, if one gets used to the decimal values that appear in the Table, calculation of decimals in divisions will become very simple. For instance, when an integer is divided by 7, the decimal values can only be .14, .28, .42, .57, .71, .85 or .00. (There are approximate values)
• This also means that the difference between two ratios like can be integral if and only if x is divisible by both 6 and 7. This principle is very useful as an advanced short cut for option based solution of some questions.
Percentage Conversion Table
Calculation of Multiplication by Numbers like 1.21, 0.83 and so on
In my opinion, the calculation of multiplication of any number by a number of the form 0.xy or of the form 1.ab should be viewed as a subtraction/addition situation and not as a multiplication situation. This can be explained as follows.
Example: Calculate 1.23 × 473.
Solution: If we try to calculate this by multiplying, we will end up going through a very time taking process, which will yield the final value at the end but nothing before that (i.e. you will have no clue
about the answer’s range till you reach the end of the calculation). Instead, one should view this multiplication as an addition of 23% to the original number. This means, the answer can be got by adding 23% of the number to itself.
Thus 473 × 1.23 = 473 + 23% of 473 = 473 + 94.6 + 3% of 473 = 567.6 + 14.19 = 581.79
(The percentage rule can be used to calculate the addition and get the answer.)
The similar process can be utilised for the calculation of multiplication by a number such as 0.87
(Answer can be got by subtracting 13% of the number from itself and this calculation can again be done by percentage rule.)




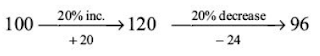











“Nice Post. It’s really a very good article. I noticed all your important points. Thanks"
ReplyDeletehow to convert decimals to fractions